流体力学

流体の性質

水の密度

　水は１気圧、4℃で体積が最大となり、密度は約1,000kg/m3となる。
正確には、1気圧3.98℃の純粋な水の密度は、1.000kg/㎥であり、水温が低いまたは高くても密度は小さくなる。また、1気圧0℃のときの密度は、999.84kg/㎥、1気圧100℃のときの密度は958.35kg/㎥である。0℃で氷になると約10%程度体積が増える。

水圧

　水中における水の圧力は、水面からの深さに比例して大きくなる。
水圧$p$は、次式で示され、深さ$h$に比例する。
$p:水圧　[Pa]$
$ρ：水の密度　[kg/㎥]$
$g:重力加速度9.8　[m/s^2]$
$h:水面からの深さ　[m]$
$p=ρgh$

粘性

　粘性とは運動している流体内部の近接した２つの部分が相互に力を及ぼす性質のことであり、内部摩擦ともいう。
摩擦応力が速度勾配に比例する流体をニュートン流体という。
一般に、水はニュートン流体として扱われ、粘性による摩擦応力は、速度勾配に比例する。

$摩擦応力＝粘性係数×速度勾配$

速度勾配＝dv/dy
速度/管壁からの距離

流体の粘性による摩擦応力の影響は、物体の表面近くで顕著であり、この物体表面近くの層を境界層という。
粘性がなく圧力のみ存在する流体を完全流体という。

粘性係数

　流体固有の粘性を表す定数であり流体の種類と温度により変わる。
水のような液体の粘性係数は、温度が高くなるにつれて減少し、圧力の増加とともに多少増加する。
一方、気体の粘性係数は、温度の上昇とともに増加する。

動粘性係数

　動粘性係数は、粘性係数を流体の密度で除した値であり、粘性係数に比例し密度に反比例する。
以下の式で表される。
動粘性係数：$ν$（ニュー）
粘性係数：$μ$（ミュー）
流体の密度：$ρ$（ロー）
$ν=\frac{μ}{ρ}$
$動粘性係数＝\frac{粘性係数}{流体の密度}$

$動粘性係数＝粘性係数÷密度$

気体は温度の上昇とともに大きくなり、液体は温度の上昇とともに小さくなる。

圧縮性

　物体に圧力を加えたときに、体積が変化する性質をいう。
液体は、圧力を加えても体積変化がほとんどない非圧縮性流体である。
気体は、圧力を加えると体積変化が大きい圧縮性流体である。

溶解度

　液体物質に溶ける物質量の上限、溶けやすさを表し、一定温度の液体に溶解する空気の量は、圧力に比例する。
水に対する空気の溶解度は、水温の上昇とともに減少する。水を加熱すると泡が発生する。

等方性

　どの方向に対しても等しい性質を有している。これをパスカルの原理という。
密閉した容器内に静止している流体の一部に加えられた圧力は、全ての方向に等しく作用する。

定常流と非定常流

　定常流とは、流れの状態が場所によってのみ定まり、時間的には変化しない流れをいう。
反対に非定常流とは、流れの状態が場所によって、時間と共に変化する流れをいう。

レイノルズ数

　レイノルズ数：Reとは、管内の流体の流れが層流か乱流かを判断する数値である。
流れの慣性力と粘性力の比で表され、平均流速と管径に比例し動粘性係数に反比例する。
層流とは、液体分子が層を成して流れることをいう。
乱流とは、流体分子が不規則に入り混じる流れをいう。

$Re＝平均流速×管径÷動粘性係数$

2,000程度より小さい状態は層流である。
4,000程度より大きい状態は乱流である。
層流から乱流に遷移するときの値を臨界レイノルズ数という。
水のレイノルズ数は温度上昇とともに大きくなる。

滑らかな円管の層流域における管摩擦係数$λ$は、レイノルズ数に反比例する。
ハーゲン・ポアズイユの式
$λ=\frac{64}{R_{e}}$

乱流域では、ブラウジウスの式で表す。
$3×10^3< Re\leqq10^5$ 内面の粗い円管においては、層流は粗度にほとんど関係ない。

流体の現象

表面張力

　液体の自由な表面では、液体は液面を縮小しようとする性質を持っている。このため液面は、弾性膜のような作用をなし表面に張力がはたらく。これを表面張力という。液体分子の凝集によって、液体の表面をできるだけ小さくしようとする力である。
液体と固体の接する角度を接触角という。

毛管現象

　液中に細い管を立てたときに、液体の表面が上昇又は下降する現象である。毛管現象は表面張力によるものであり、細管中の液面高さは表面張力に比例する。

ウォーターハンマー

　管内を流れる流体の密度が大きいほど、管路閉止時の水撃圧は高くなる。
弁を急に閉めた時に生じる圧力上昇$h_{max}[Pa]$は、ジェーコフスキーの式により求める。
$P_{0}:流体の密度[kg/㎥]$
$a:圧力波の伝播速度[m/s]$
$V_{0}:水の当初の流速[m/s]$
$h_{max}=P_{0}aV_{0}$
の式より、水撃圧は流体の密度に比例する。

　ウォーターハンマーの圧力上昇は、圧力波の伝播速度に関係する。圧力波の伝播速度は管材の縦弾性係数（ヤング率）に関係し、ヤング率が小さいほど圧力波の伝播速度が小さくなり、ウォーターハンマーが発生しづらくなる。

$a:圧力波の伝播速度[m/s]$
$a_{0}:液中音速[m/s]$
$ρ_{0}:水の密度[kg/㎥]$
$E:管材料の縦弾性係数（ヤング率）[Pa]$
$D:管の内径[m]$
$S:管の肉厚[m]$

$a=\frac{a_0}{\sqrt{(1+a^2_{0}ρ_0D/ES} \\}$

鋼管よりも硬質塩化ビニル管の方が、ウォータハンマが発生しにくいのは、ヤング率が鋼管よりも硬質塩化ビニル管の方が小さいからである。

キャビテーション

　キャビテーションとは、流体が流動しているときに、ある部分における静圧がそのときの流体温度に相当する蒸気圧力（飽和蒸気圧）以下になった場合に、その部分の液体が局部的に蒸発を起こし気泡を発生する現象をいう。また、水温が高いと水は蒸発気化しやすくなるので、キャビテーションが発生しやすくなる。

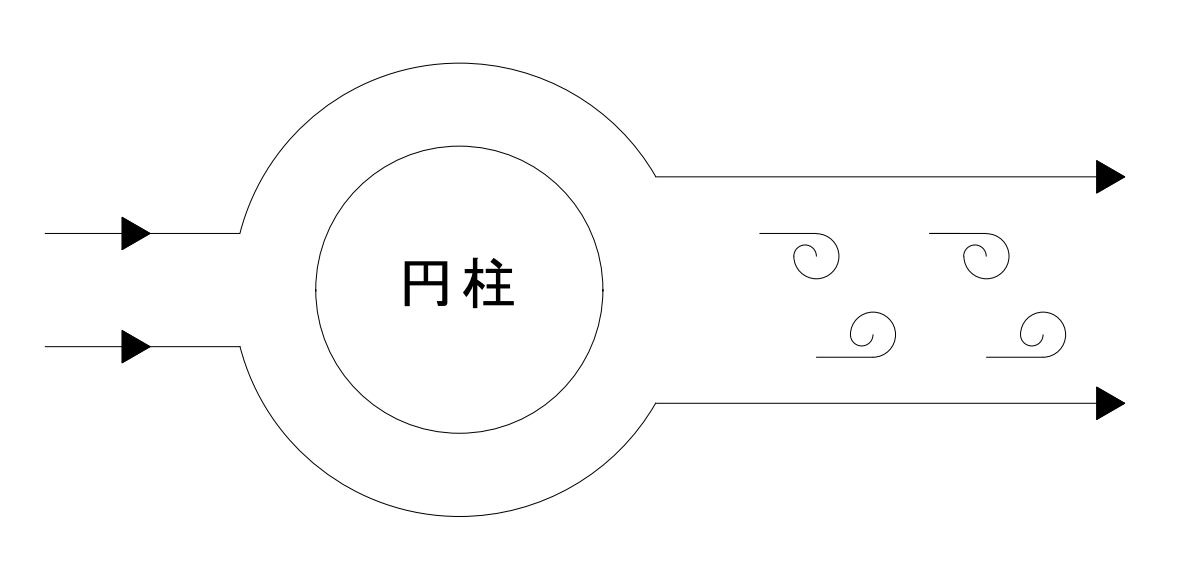
カルマン渦

　カルマン渦とは、一様な流れの中に置いた円柱などの下流側に交互に発生する渦のことをいう。カルマン渦が発生すると、物体の左右で渦が交互に発生するため、物体が振動する。

流体に関する一覧表

流体の運動
名称	数式及び注意点
摩擦応力	摩擦応力＝粘性係数×速度勾配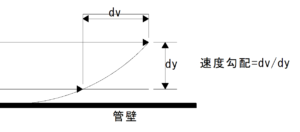
	摩擦応力は速度勾配に比例する
	粘性係数は、気体では温度の上昇とともに大きくなり、液体では温度の上昇とともに小さくなる。
動粘性係数	動粘性係数＝粘性係数÷密度	$ν=\frac{η}{ρ}$
	動粘性係数は、粘性係数に比例し、密度に反比例する。
レイノルズ数	レイノルズ数＝平均流速×管径÷動粘性係数	$Re=$$\frac{V×d}{ν}$
	層流か乱流かを判断する数値　層流<2,000　乱流>4,000
	慣性力（平均流速×管径）と粘性力（動粘性係数）の比で表す。
	レイノルズ数は、平均流速と管径に比例し、動粘性係数に反比例する。
トリチェリの定理	流速＝速度係数$\sqrt{2×重力加速度×水面の高さ}$	$ν=C\sqrt{2gh} \\$
	水槽の下端の小穴から流出する水の速度$ν$は、小穴から水面までの高さ$h$の1/2乗に比例する。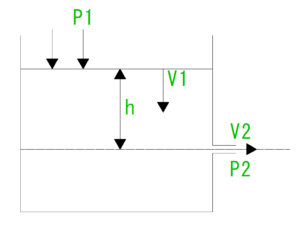
静圧	静圧＝全圧－動圧	$P$$S$$＝$$P$$T$$-P$$D$
動圧	動圧＝（流体の密度×流体の速度の2乗）÷2	$P$$D$$=\frac{ρ×ν^2}{2}$
全圧	全圧＝静圧＋動圧	$P$$T$$=P$$S$$+P$$D$
圧力損失	圧力損失＝（管摩擦係数×管長÷管径）×（密度×平均流速の2乗÷2）	$⊿P＝λ\frac{l}{d}$$×$$\frac{ρ×ν^2}{2}$
	ダルシー・ワイスバッハの式
	管摩擦係数、管長、平均流速の2乗に比例する。
	管径に反比例する。
水頭損失	水頭損失＝（管摩擦係数×管長÷管径）×（平均流速の2乗÷2×重力）	$⊿h＝λ\frac{l}{d}$$×$$\frac{ν^2}{2g}$
	動圧に比例する。