ダルシー・ワイズバッハの式
管路計算
ベルヌーイの定理・トリチェリの定理
計測機器
静圧・動圧・全圧
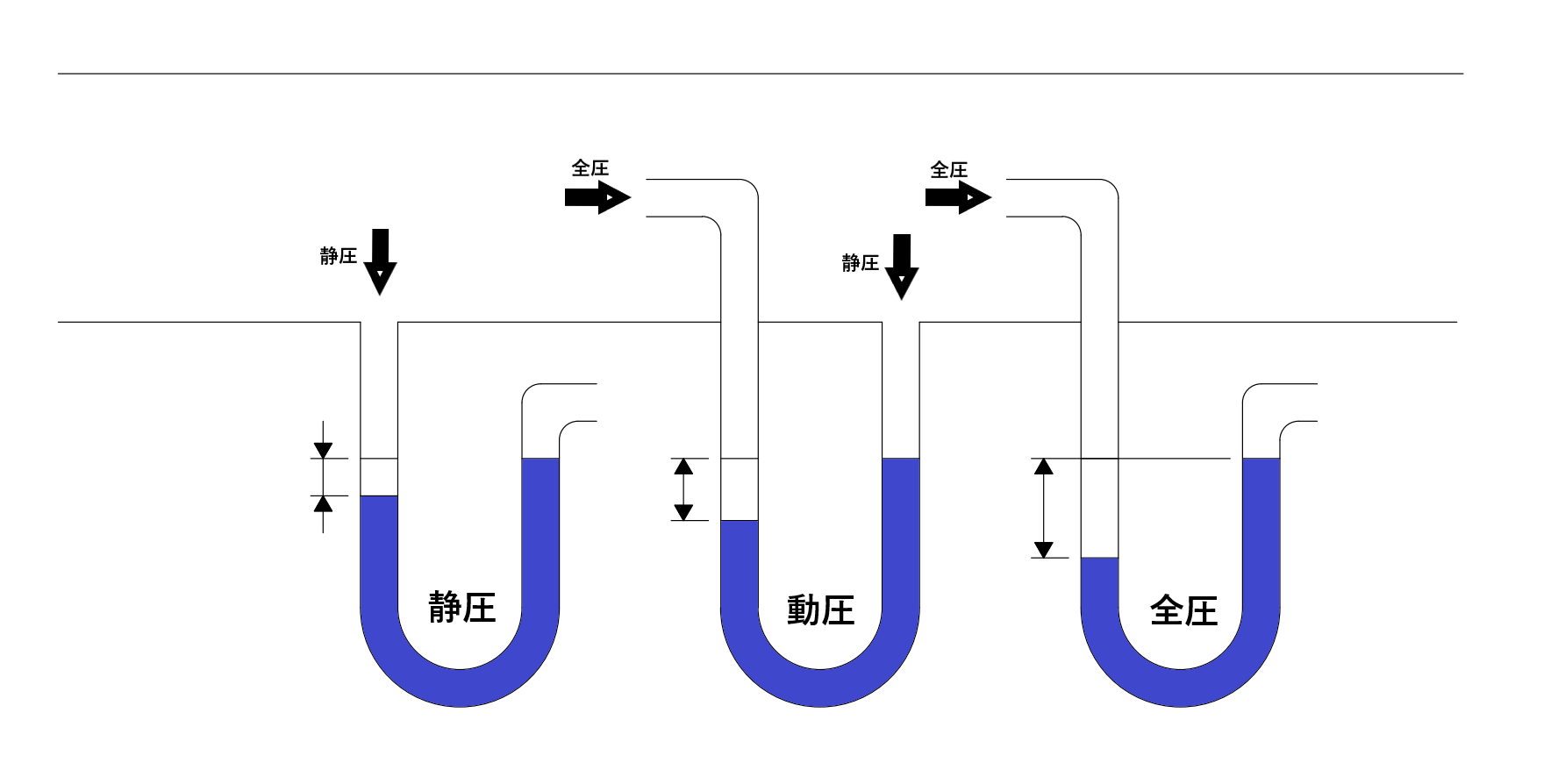
静圧:$P_S$は、運動流体では、流れに平行な面に垂直に作用する。
動圧:$P_D$は、運動している流体の全圧と静圧の差で表す。
$P_D=\frac{ρv^2}{2} \\$
全圧:$P_T$は、運動している流体が有している圧力の総和である。
$P_T=静圧+動圧=P_S+P_D$
$=P_S+\frac{ρv^2}{2}$
ダルシー・ワイズバッハの式
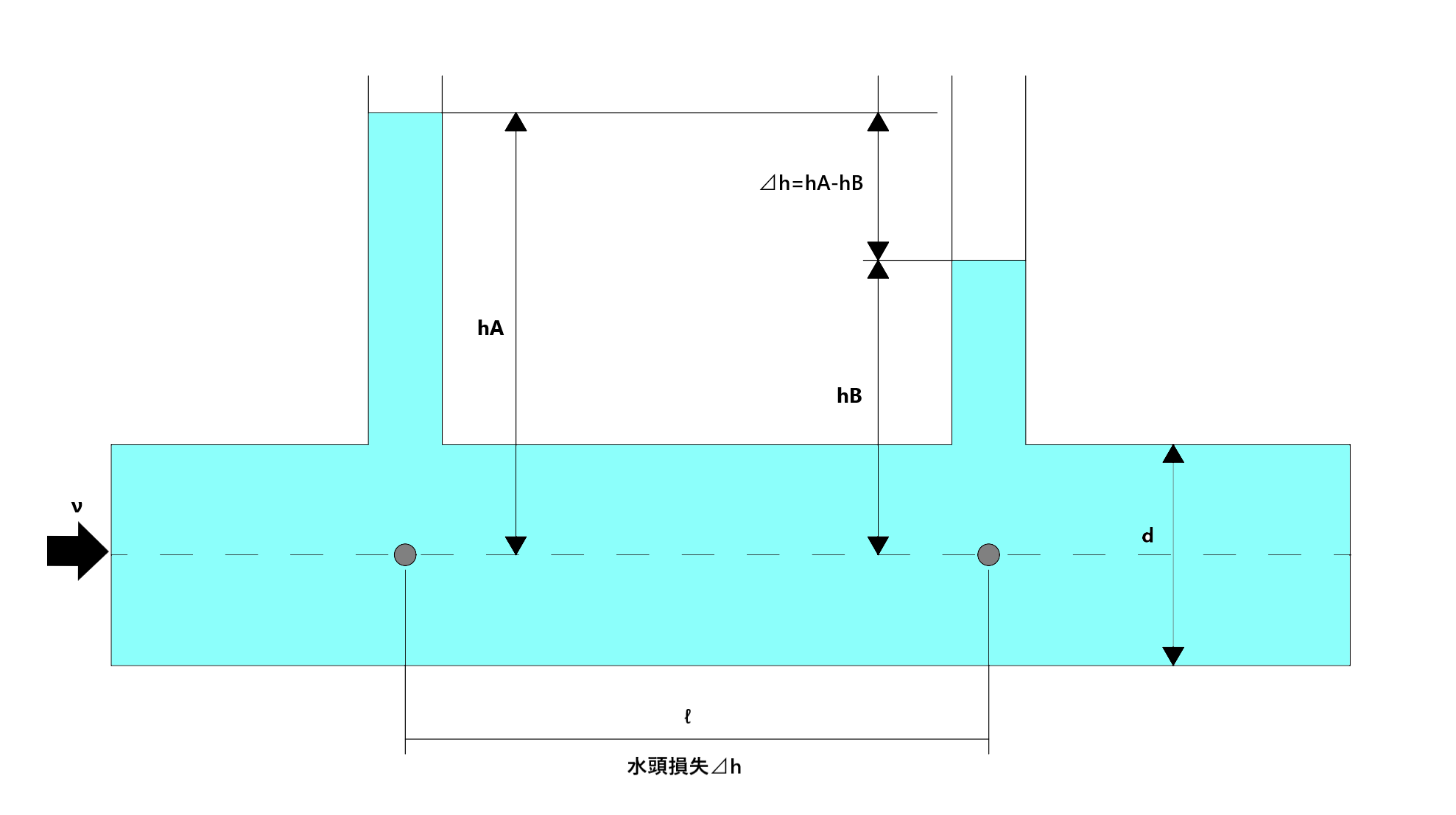
水頭損失:$⊿h$
管摩擦係数:$λ$
管長:$l$
管径:$d$
平均流速:$v$
流体の密度:$ρ$
動圧$(ρv^2)÷2$
$⊿h=h_A-h_B=λ\frac{l}{d}×\frac{v^2}{2g}$
圧力損失:$⊿P$(水頭損失:$⊿h$)
$⊿P=P_A-P_B=λ\frac{l}{d}×\frac{ρv^2}{2}$
流体が運動するときは、粘性のために流体と流体との間に内部摩擦、流体と固体との間に外部摩擦が働く。圧力損失は動圧に比例し管径$d$に反比例する。
管路計算
図に示す水平な管路内を空気が流れる場合において、A点とB点の間の圧力損失⊿Pの値として適当なものはどれか。
ただし、A点における全圧は80Pa、B点の静圧は10Pa、B点の流速は10m/s、空気の密度は1.2kg/㎥とする。
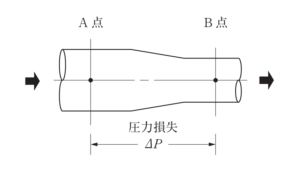
⑴5Pa
⑵10Pa
⑶15Pa
⑷20Pa
例題解答
| 測点 | A点 | B点 |
| 全圧(PT) | 80Pa | 70Pa |
| 静圧(Ps) | 10Pa | |
| 動圧(PD) | 60Pa | |
| 流速(m/s) | 10m/s | |
| 密度(kg/㎥) | 1.2kg/㎥ | |
| 圧力損失⊿P | 10Pa | |
$動圧=密度×速度の2乗÷2$
$B点の動圧=1.2×10^2÷2=60Pa$
$B点の全圧=静圧+動圧=10Pa+60Pa=70Pa$
$圧力損失⊿P=A点の全圧-B点の全圧$
$80Pa-70Pa=10Pa$
正解:⑵
定理
ベルヌーイの定理
ベルヌーイの定理は、重力の場において、定常流である非圧縮性の完全流体に適用されるエネルギー保存則であり、流体のもっているエネルギーの総和は流線に沿って一定不変である。流体の粘性と圧縮性は考慮していない。
$\frac{ρv^2}{2}+P+ρgh=一定$
運動エネルギー+圧力のエネルギー+位置のエネルギー=一定
$v$:速度
$g$:重力加速度
$P$:圧力
$h$:基準面の鉛直方向の高さ
$ρ$:流体の密度
トリチェリの定理
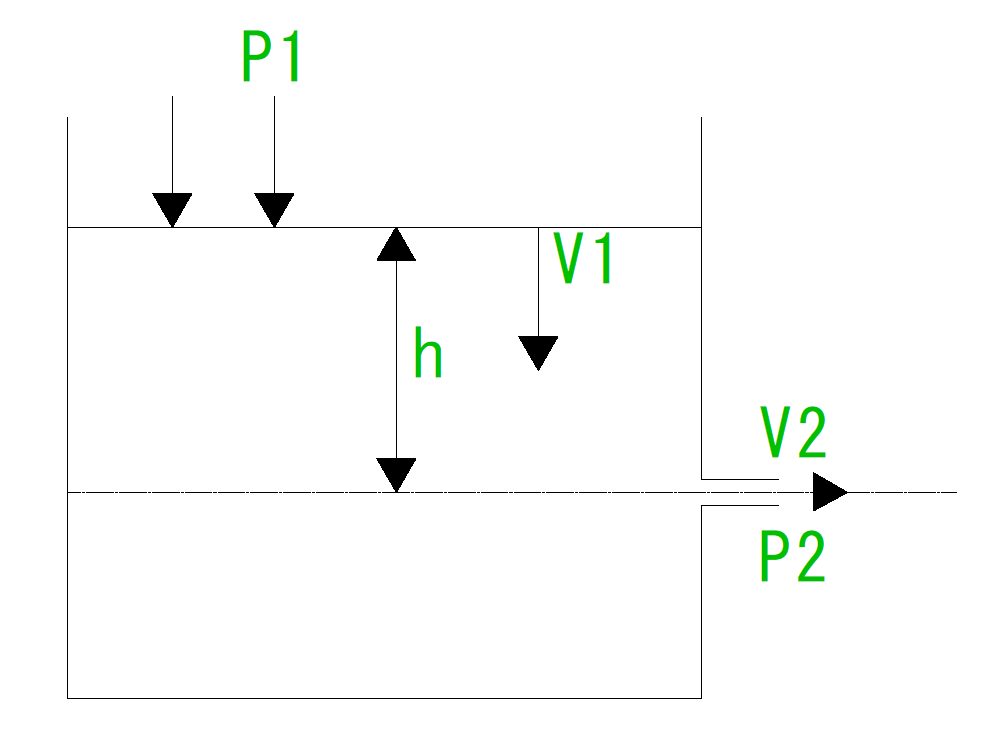
大きな水槽の側壁に儲けた小穴から流出する水の速度$v$と、小穴から水面までの高さ$h$の関係を表す。
$v=\sqrt{2gh} \\$
$g$:重力加速度
水の速度は水槽の小穴から水面までの高さの1/2乗に比例するため、液面の高さを3倍にすると流速は$\sqrt{3} \\$倍になる。
オリフィス等で流量測定を行う場合は、次式での算定をする。
$v=C\sqrt{2gh} \\$
$C$:速度係数
流量計
| 流量計 | |
| ピトー管 | 管内の全圧と静圧の差、動圧を測定して流量を算出する。 |
| ベンチュリー管 | 大口径部の静圧と小口径部の静圧の差を測定することにより流量を算出する。 |
| オリフィス流量計 | オリフィスの前後の静圧の差を測定することにより流量を算出する。 |
ピトー管
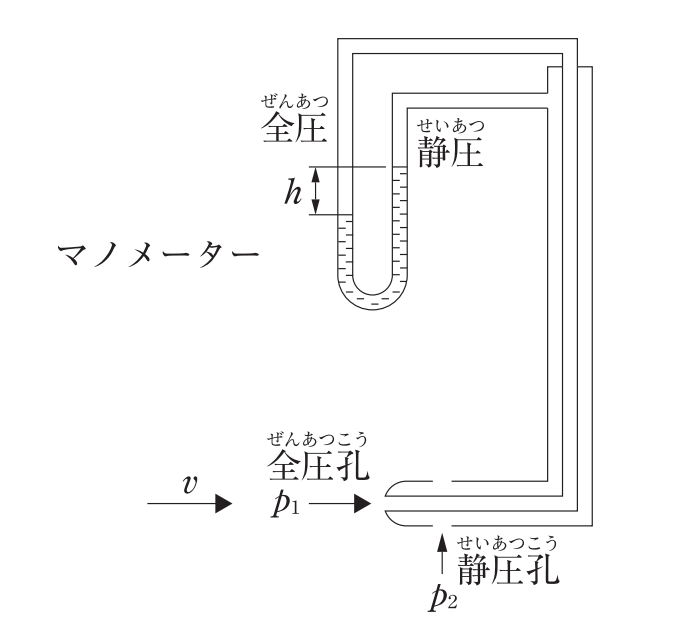
全圧と静圧の差(=動圧)を測定し、流速を算出する。
ベンチュリー管
大口径部と小口径部の静圧の差を測定し、流量を算出する。
オリフィス流量計
オリフィス前後の静圧を測定し流量を算出する。
