熱力学

熱

用語と関係性一覧

用語	効果・法則等
熱力学の第一法則	エネルギー保存則
熱力学の第二法則	エントロピー
熱伝導	フーリエの法則
熱伝達	ニュートンの冷却則
熱放射	ステファン・ボルツマン定数
熱機関	カルノーサイクル
熱起電力	ゼーベック効果
電子冷凍	ペルチェ効果
モリエ線図	冷凍サイクル
気体の状態式	ボイル・シャルルの法則

熱力学の法則

第１法則
　ある熱力学的系とその周囲との総エネルギー量は，たとえそのエネルギーがいろいろ形をかえても，つねに一定に保たれるという法則である。この法則から，状態がかわったことに伴うエネルギー量の変化は最初の状態と最後の状態のみで決まり，各状態にその状態によってのみ決まる固有のエネルギー量を考えることができ，内部エネルギーが定義される．このことから、熱と仕事のエネルギーは相互に変換可能であり、変換の前後でエネルギーの総和が一定である。

第２法則
　熱が低温度の物体から、高温度の物体へ自然に移ることはなく、クロジュース（クラウジウス）の原理という。

顕熱と潜熱

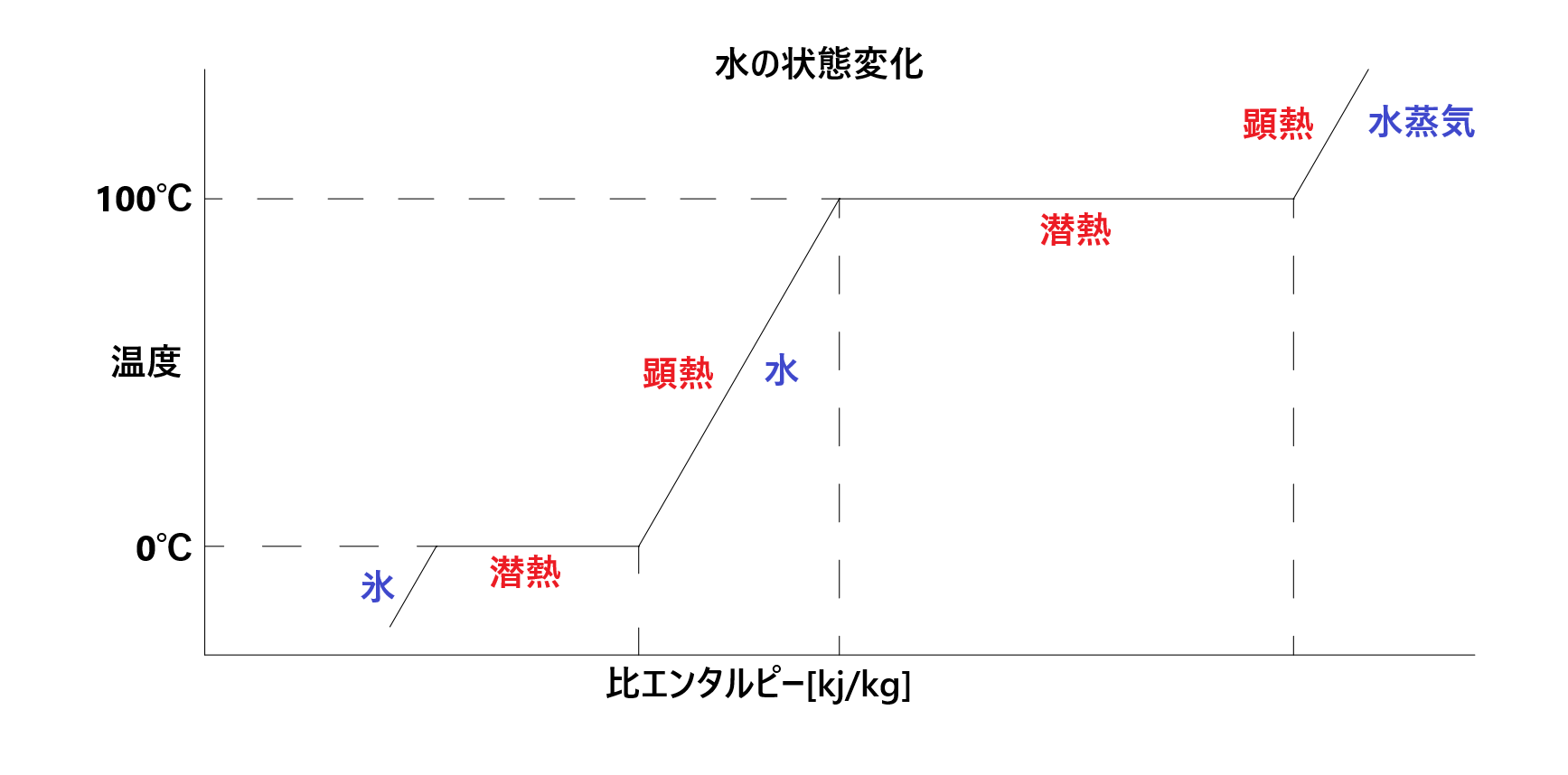
　顕熱とは、物体の温度を変化させる熱であり、潜熱とは、融解熱、気化熱等のように物体の相を変化させる熱である。

比熱

比熱	固体・液体の比熱	気体の比熱
定容比熱：$C$$v$ 定圧比熱：$C$$p$	$C$$p$$≒C$$v$	$C$$p$$＞C$$v$
比熱比=定圧比熱÷定容比熱	$C$$p$$/C$$v$	$C$$p$$/C$$v$ （１より大きい）

　圧力一定のもとでの比熱を定圧比熱$C_P$といい、容積一定のもとでの比熱を定容比熱$C_V$という。
固体や液体は$C_p \fallingdotseq C_V$となり、気体は$C_P>C_V$となる。

比熱比とは定圧比熱を定容比熱で除した値であり、気体では常に1より大きい。
$C_p÷C_V$
気体は$1 < C_p÷C_V$

気体の法則

　ボイルの法則は、温度が一定のとき、一定質量の圧力Pと体積Vの積は一定を表す。
$PV=一定$

シャルルの法則

　圧力が一定のとき、気体の体積変化の割合は、温度変化に比例する。

ボイル・シャルルの法則

　一定質量の気体の体積Vは、圧力Pに反比例し、温度Tに比例する。

$\frac{PV}{T}=一定$

気体の状態式であり、ボイル・シャルルの法則に従う気体を理想気体という。

　気体を断熱圧縮した場合は、温度が上昇し、断熱膨張させた場合は温度が低下する。断熱圧縮で$P$（圧力）が上昇すると、$T$（温度）が大きくなる。逆に$P$（圧力）が下がると、$T$（温度）が小さくなる。エンタルピーは、物質の持つエネルギーの状態量の一つで、その物質の内部エネルギーに、外部への体積膨張仕事量を加えたもので表される。

ダルトンの分圧の法則

　混合気体の圧力は、混合前の各気体の圧力の和に等しい。

気体A（$P_A$）
気体B（$P_B$）
気体C（$P_C$）
混合気体（$P_A+P_B+P_C$）

膨張

　温度が１℃上昇後の物体の体積を温度上昇前の物体の体積で除した値を体膨張係数という。温度が１℃上昇後の物体の長さを温度上昇前の物体の長さで除した値を線膨張係数という。
等方性を有する物体は、$体膨張係数　\fallingdotseq　線膨張係数×3$

相変化

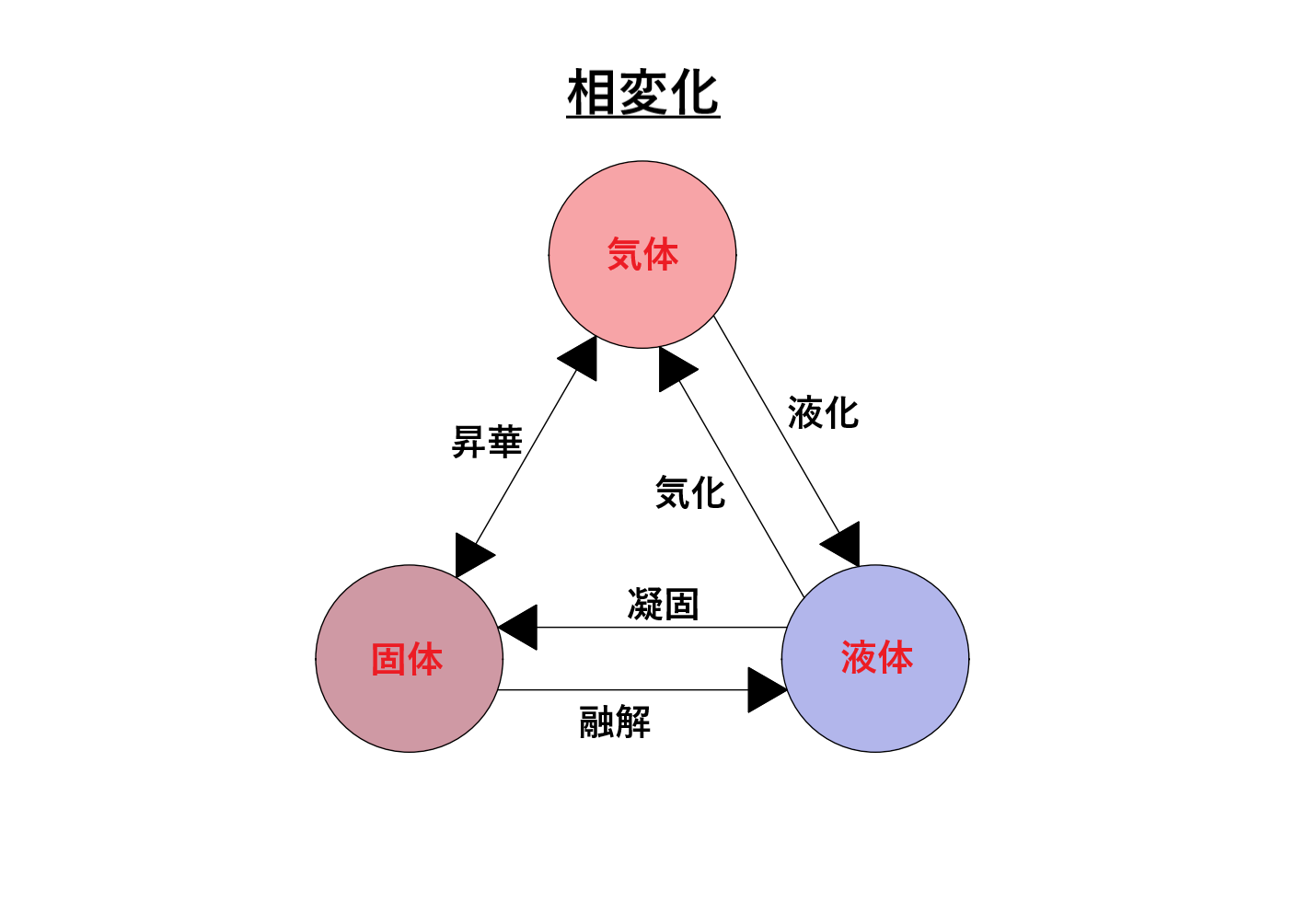
　物質が化学的，物理的に一様であるとき，その均質な部分を相と呼ぶが，一般に物質は，例えば水(液相)が氷(固相)になったり水蒸気(気相)になったりするように，温度や圧力などによって異なる相をとる。このように，物質がある相から異なる相に移ることを相転移，または相変化という。単に転移ということもある。

固体から液体　融解
液体から固体　凝固
液体から気体　気化
気体から液体　液化
固体から気体　昇華
気体から固体　昇華

単一物質　融解店＝凝固点、沸点＝凝縮点

ゼーベック効果

　ゼーベック効果は、2種類の金属を接合した回路の一方の接点を加熱して他方を冷却すると、接点間に熱起電力を生じる。

ペルチェ効果

　2種類の金属を接合した回路に電圧をかけると、一方の接点の温度が上がり他方が下がる。これをペルチェ効果という。

伝熱

熱伝導

　固体内部及び隣接する固体間で、高温部から低温部に熱が移動する現象である。

フーリエの法則　熱移動量$Q$
$Q=λ\frac{θ_1-θ_2}{d}Aτ$

$λ$(ラムダ):熱伝導率
$θ_1$:高温側壁面温度
$θ_2$:低温側壁面温度
$d$:壁の厚さ
$A$:壁面積
$τ$(タウ):時間

　熱移動量$Q$は、熱伝導率$λ$に比例し、温度勾配$(θ_1-θ_2)/d$に比例する。
熱移動量$Q$が一定時の温度勾配$(θ_1-θ_2)/d$は、熱伝導率$λ$に反比例する。

熱伝達

熱伝達とは、固体とこれに接する流体の間を熱が移動する現象である。

$Q=α(θ-t)Aτ$

$α$:熱伝達率
$θ$:壁面温度
$t$:周囲流体温度
$A$:壁面積
$τ$:時間

$α$は、材料の表面と空気の間で、熱伝達するときの熱量の割合
熱移動量$Q$は、固体表面温度と、周囲流体温度のとの差$(θ-t)$に比例する。
固体壁表面の熱伝達率の大きさは、固体壁表面に当たる気流の影響を受ける。
強制対流熱伝導とは、外的駆動力による強制対流時の流体と壁面の間の熱移動現象をいう。

熱放射

　熱放射とは物体が電磁波の形で、熱エネルギーを放出・吸収する現象である。
熱の移動は媒体を必要とせず、真空中でも移動する。熱移動量は、ステファン・ボルツマンの法則で物体表面の絶対温度の４乗に比例する。放射の強さは、物体の温度と表面の性質で決まる。

熱対流

　流体内のある部分が温められると、膨張により密度を減じて上昇し、周囲の低温流体が下降する現象である。固体と流体が接しているとき、固体から一定範囲の薄い流体層を温度境界層という。熱の浮力により発生する自然対流があり、外力により発生する対流を強制対流という。強制対流は、自然対流より、熱移動量が多く温度境界層が薄い。自然対流は、流体温度の異なる部分の密度差により浮力を生じ、上昇流と下降流が起こることで生じる。

熱通過（熱貫流）

　熱貫流は、壁の片側にある流体の熱が、もう一方にある流体に伝わる現象である。
$Q=K(t_1-t_2)Aτ$

$K$:熱通過率（熱貫流率）
$t_1,t_2$:両側の流体温度
$A$:壁面積
$τ$:時間

熱移動量$Q$は、両側流体間の温度差$(t_1-t_2)$に比例する。
熱通過率$K$は、固体壁の厚さに反比例しない。

燃焼

燃焼現象

　排気ガス中に二酸化炭素と水蒸気以外の可燃物を含まない燃焼を完全燃焼という。
不完全燃焼の排ガスは、一般に、二酸化炭素、水蒸気、窒素のほか一酸化炭素などが含まれている。
酸素濃度が19%に低下すると不完全燃焼をおこす。・二酸化炭素の熱解離は、火炎温度の上昇を抑制する。

窒素酸化物(NOx)

　燃料中の窒素成分が酸素と結びついて発生すし、燃焼ガス中の窒素酸化物は、低温燃焼時より高温燃焼時の方が多い。高温下の空気中、窒素と酸素の結合で発生する。

理論空気量

　理論空気量とは燃料を完全燃焼するために、理論的に必要な最少空気量をいう。気体燃料は、固体燃料より、理論空気量に近い空気量で完全燃焼し、気体燃料は、液体燃料より、理論空気量に近い空気量で完全燃焼する。
単位量の燃料が理論空気量で完全燃焼したときに生成するガス量を、理論燃焼ガス量という。

空気過剰率

$m=\frac{供給された空気量}{理論空気量}$

　適正値は、気体燃料＜液体燃料＜固体燃料となる。
空気過剰率が小さすぎると不完全燃焼となり、大きすぎると廃ガスによる熱損失が増大する。完全燃焼する範囲で小さくすることが必要である。
ボイラーの燃焼において、熱損失を少なくするため、完全燃焼する範囲において空気過剰率を少なくすることが望ましい。

発熱量

　燃焼により生じる水蒸気の潜熱分を含んだ発熱量であり、高発熱量（総発熱量、高位発熱量）で表す。燃焼により生じる水蒸気の潜熱分を除いた発熱量は低発熱量（低位発熱量）となる。ガスの単位体積当たりの総発熱量をガスの比重の平方根で除したものを、ウォッペ指数といい、ガスの発熱量は、一般に高発熱量で表示する。水蒸気の潜熱は熱機関では利用できない。

$高発熱量＝低発熱量＋水蒸気の潜熱$

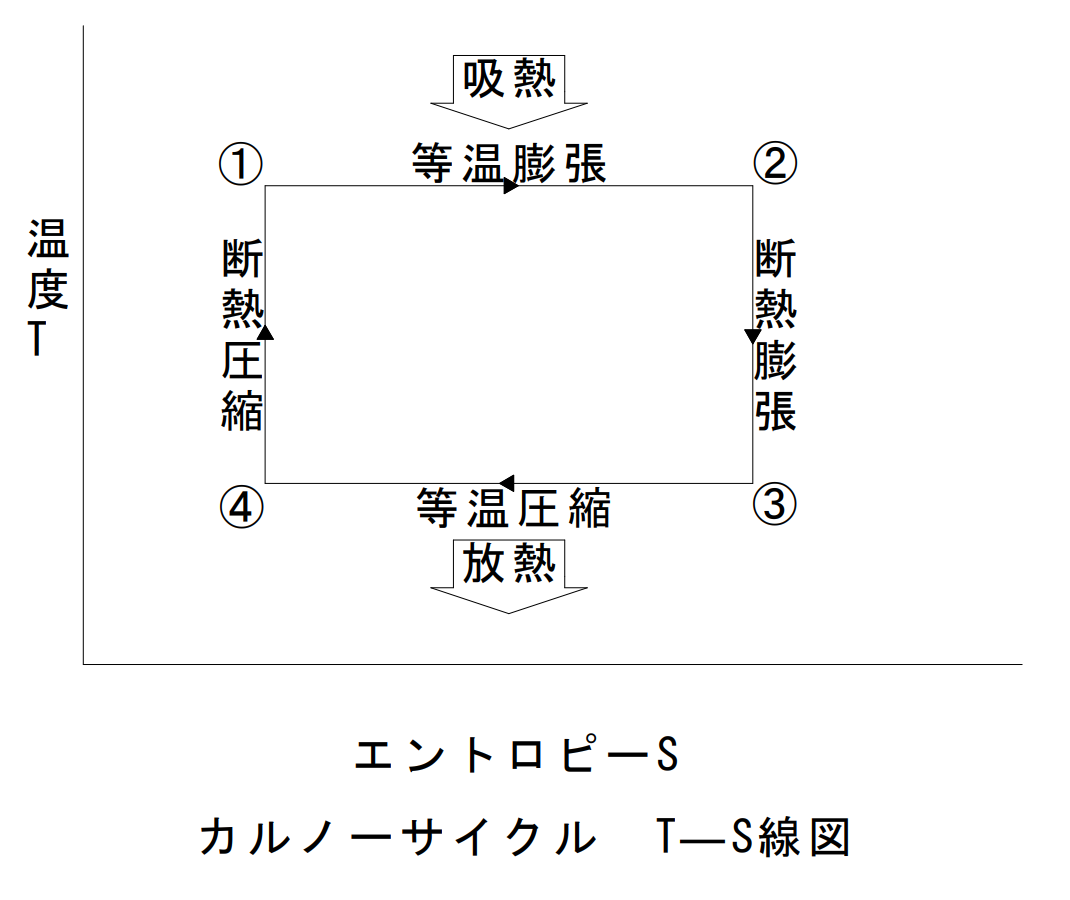
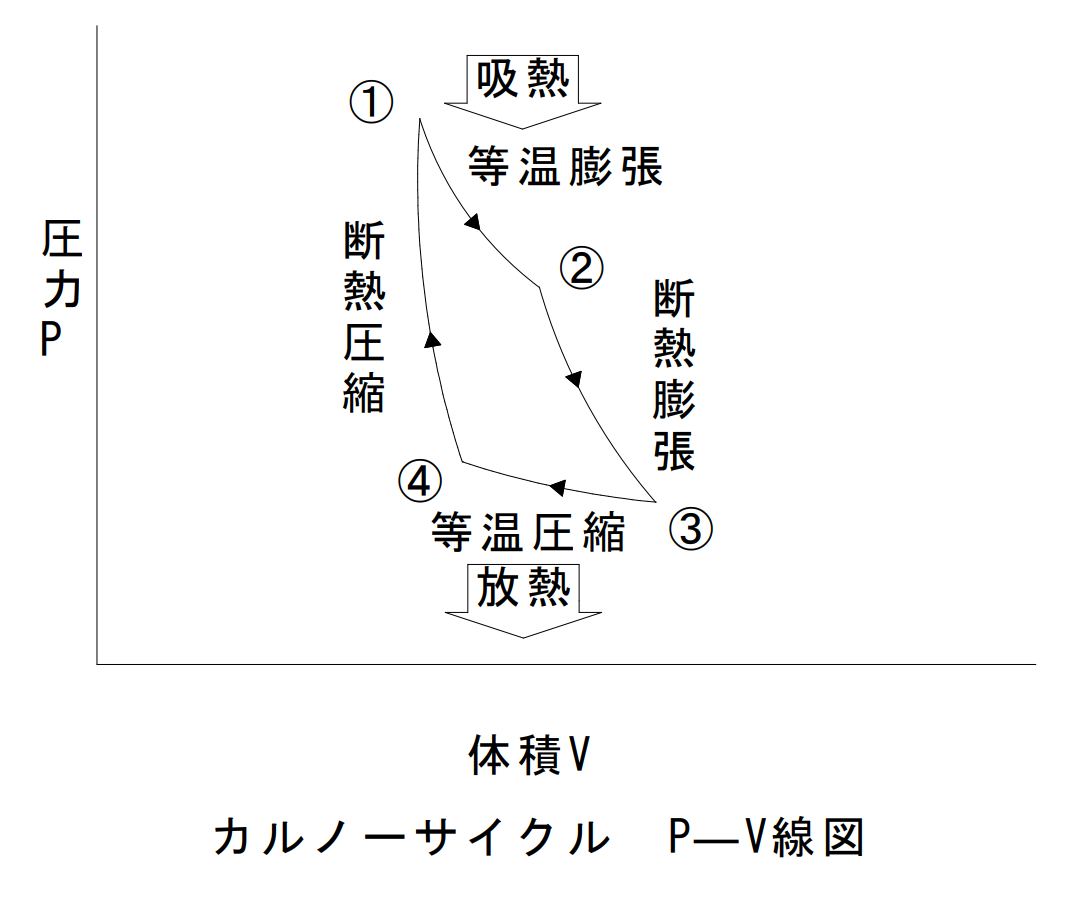
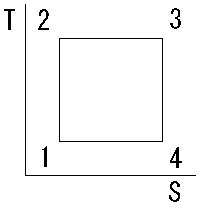
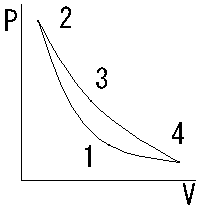
カルノーサイクル

　カルノーサイクルは、等温膨張、断熱膨張、等温圧縮、断熱圧縮の四つの可逆過程から構成され、高温熱源と低温熱源の温度差が大きいほど効率が高くなる。実用機関には存在しない理想的な熱機関の可逆サイクルであり、逆回転はカルノーの冷凍サイクルである。

名称	サイクル	温度T	エントロピーS	圧力P	体積V
等温膨張	①→②	一定	上がる	下がる	膨張
断熱膨張	②→③	下がる	一定	下がる	膨張
等温圧縮	③→④	一定	下がる	上がる	圧縮
断熱圧縮	④→①	上がる	一定	上がる	圧縮

冷凍

　冷凍とは、製氷、食品の冷蔵、空気調和などのために、物体や気体などから熱を奪って、周囲の大気温度より低い所定の温度に冷却・維持することである。冷媒による冷凍とは蒸発しやすい冷媒液を低温で蒸発させ、蒸発熱（潜熱）を冷凍すべき物体から奪うことであり、現在、冷凍に広く使用されている冷媒には、アンモニア、フロン、ハイドロカーボン、水などがある。
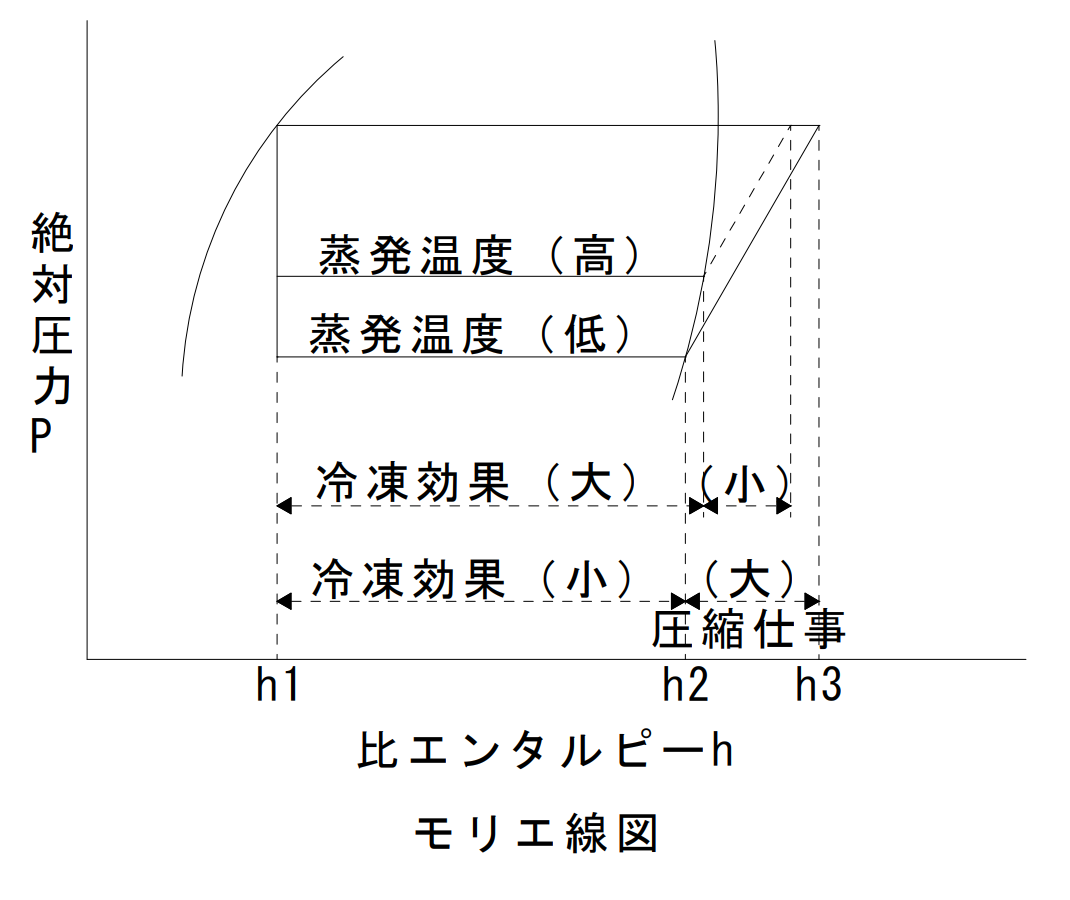
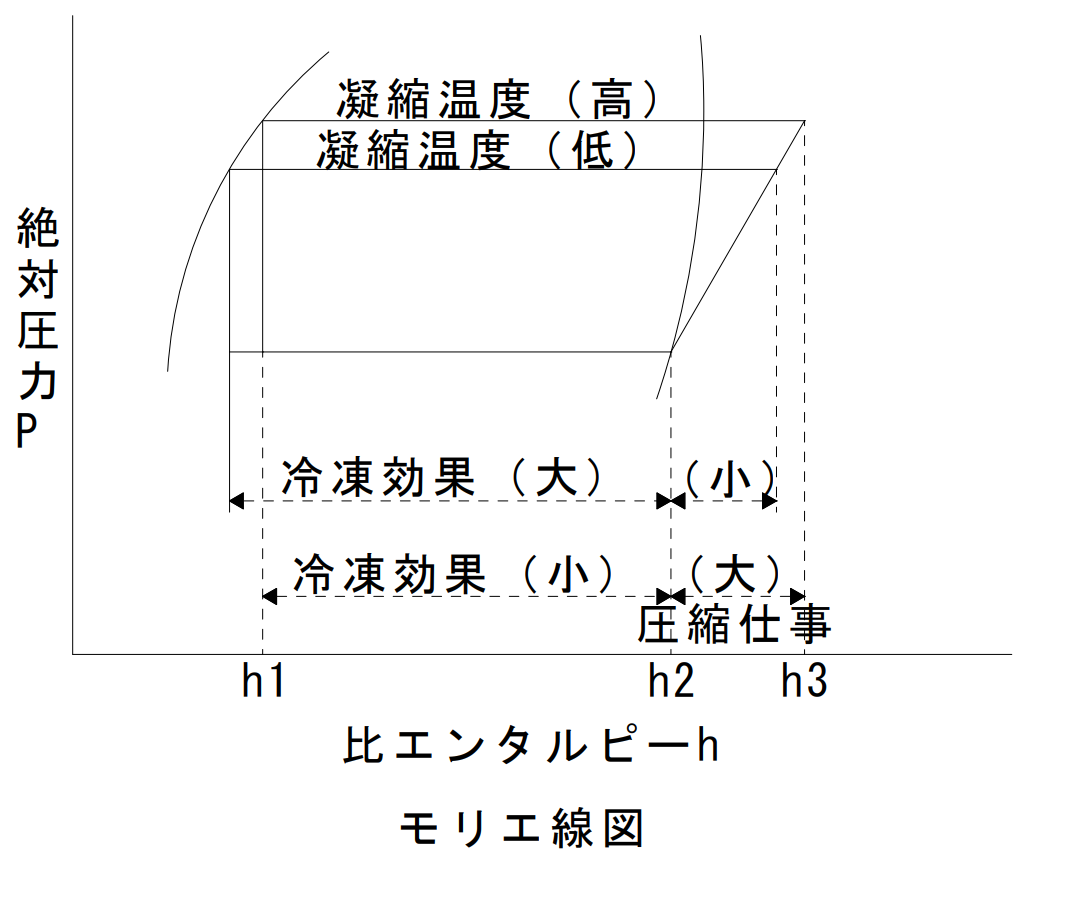
モリエ線図は、冷媒の特性を分析する場合などに用いられ、冷凍サイクル状態変化を表す。

前提条件	凝縮温度	蒸発温度	圧縮仕事	冷凍効果	成績係数
蒸発温度一定	低	―	小	大	大
	高	―	大	小	小
凝縮温度一定	―	低	大	小	小
	―	高	小	大	大

成績係数

$ε_C(イプシロン)=(h_2-h_1)÷(h_3-h_2)$
$=冷凍効果÷圧縮仕事$
凝縮器の凝縮温度が低くなった状態は、冷凍効果は大きくなる。

湿り空気

絶対湿度

$=\frac{水蒸気の質量}{乾き空気の質量}[kg/kg(DA)]$

相対湿度

$=\frac{水蒸気分圧}{飽和水蒸気分圧}×100$[%]

エンタルピー

物体の保有する熱量の総和である。

熱水分比

　熱水分比とは、湿り空気の状態変化における比エンタルピーの変化量の絶対湿度の変化量に対する比をいう。
$比エンタルピーの変化量÷絶対湿度の変化量$

顕熱比

　顕熱比とは、全熱の変化量と顕熱の変化量との比をいう。
$顕熱÷全熱=顕熱÷(顕熱÷潜熱)$

水蒸気分圧

　水蒸気分圧とは、水蒸気が示す分圧である。湿り空気の全圧は、その湿り空気中の乾き空気の分圧と水蒸気の分圧の和で表され、飽和湿り空気の水蒸気分圧は、その温度における飽和蒸気圧と等しい。飽和湿り空気では、乾球温度と湿球温度は等しい。

露点温度

　露点温度とは、湿り空気中の水蒸気分圧（絶対湿度）に等しい水蒸気分圧（絶対湿度）をもつ飽和湿り空気の温度である。

湿り空気線図

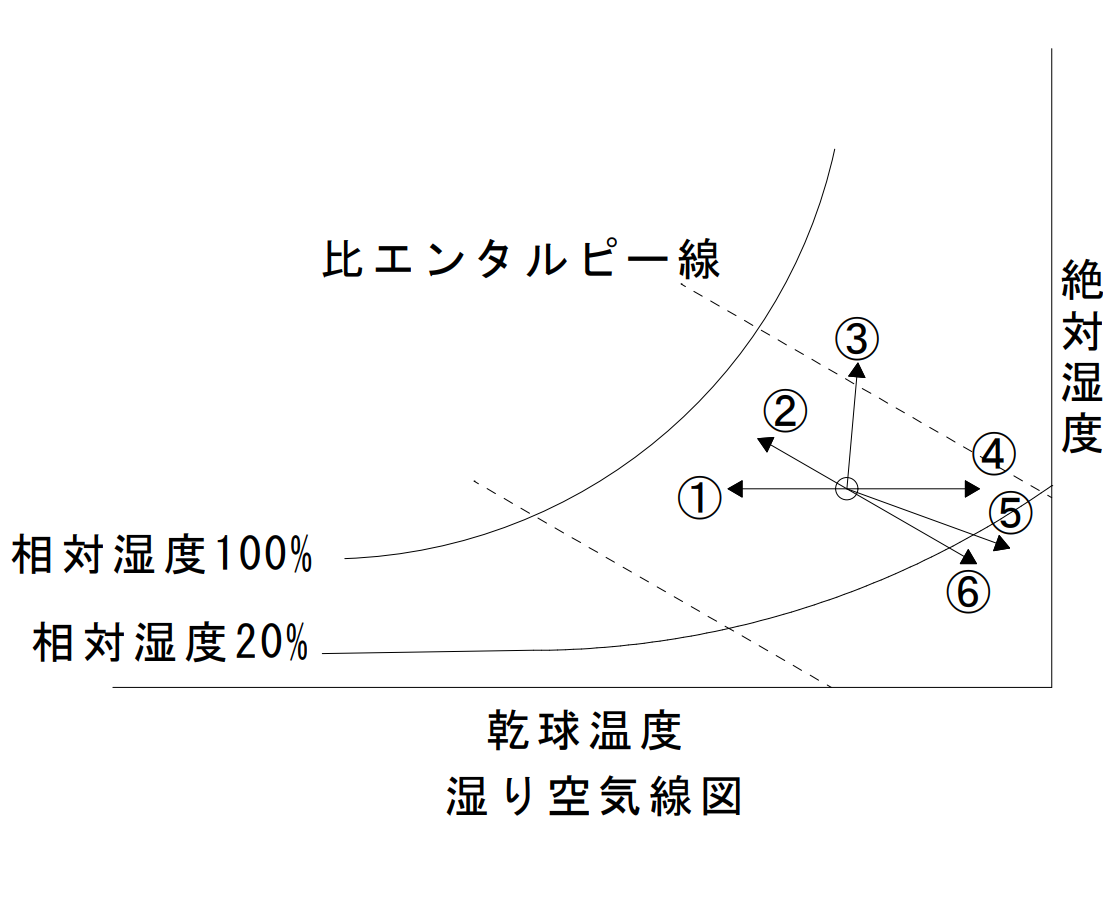
	乾球温度	湿球温度及び比エンタルピー	絶対湿度	相対湿度
①冷水コイル	下がる	下がる	不変	上がる
②水スプレー	下がる	ほぼ一定	上がる	上がる
③蒸気スプレー	上がる	上がる	上がる	上がる
④温水コイル	上がる	上がる	不変	下がる
⑤固体吸着減湿	上がる	上がる	下がる	下がる
⑥液体吸収減湿	上がる	ほぼ一定	下がる	下がる