令和2年度A[問題 No.5]
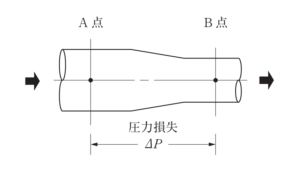
[問題 No.5]図に示す水平な管路内を空気が流れる場合において、A点とB点の間の圧力損失⊿Pの値として適当なものはどれか。
ただし、A点における全圧は80Pa、B点の静圧は10Pa、B点の流速は10m/s、空気の密度は1.2kg/㎥とする。
⑴5Pa
⑵10Pa
⑶15Pa
⑷20Pa
令和2年度A[問題 No.5]解答
| 測点 | A点 | B点 |
| 全圧(PT) | 80Pa | 70Pa |
| 静圧(Ps) | 10Pa | |
| 動圧(PD) | 60Pa | |
| 流速(m/s) | 10m/s | |
| 密度(kg/㎥) | 1.2kg/㎥ | |
| 圧力損失⊿P | 10Pa | |
$動圧=密度×速度の2乗÷2$
$B点の動圧=1.2×10^2÷2=60Pa$
$B点の全圧=静圧+動圧=10Pa+60Pa=70Pa$
$圧力損失⊿P=A点の全圧-B点の全圧$
$80Pa-70Pa=10Pa$
| 流体の運動 | ||
| 名称 | 数式及び注意点 | |
| 摩擦応力 | 摩擦応力=粘性係数×速度勾配 | 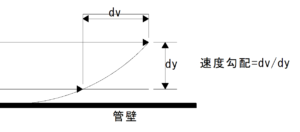 |
| 摩擦応力は速度勾配に比例する | ||
| 粘性係数は、気体では温度の上昇とともに大きくなり、液体では温度の上昇とともに小さくなる。 | ||
| 動粘性係数 | 動粘性係数=粘性係数÷密度 | $ν=\frac{η}{ρ}$ |
| 動粘性係数は、粘性係数に比例し、密度に反比例する。 | ||
| レイノルズ数 | レイノルズ数=平均流速×管径÷動粘性係数 | $Re=$$\frac{V×d}{ν}$ |
| 層流か乱流かを判断する数値 層流<2,000 乱流>4,000 | ||
| 慣性力(平均流速×管径)と粘性力(動粘性係数)の比で表す。 | ||
| レイノルズ数は、平均流速と管径に比例し、動粘性係数に反比例する。 | ||
| トリチェリの定理 | 流速=速度係数$\sqrt{2×重力加速度×水面の高さ}$ | $ν=C\sqrt{2gh} \\$ |
| 水槽の下端の小穴から流出する水の速度$ν$は、小穴から水面までの高さ$h$の1/2乗に比例する。 | 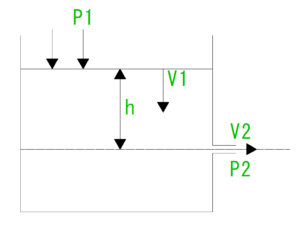 |
|
| 静圧 | 静圧=全圧-動圧 | $P$$S$$=$$P$$T$$-P$$D$ |
| 動圧 | 動圧=(流体の密度×流体の速度の2乗)÷2 | $P$$D$$=\frac{ρ×ν^2}{2}$ |
| 全圧 | 全圧=静圧+動圧 | $P$$T$$=P$$S$$+P$$D$ |
| 圧力損失 |
圧力損失=(管摩擦係数×管長÷管径)×(密度×平均流速の2乗÷2) | $⊿P=λ\frac{l}{d}$$×$$\frac{ρ×ν^2}{2}$ |
| ダルシー・ワイスバッハの式 | ||
| 管摩擦係数、管長、平均流速の2乗に比例する。 | ||
| 管径に反比例する。 | ||
| 水頭損失 |
水頭損失=(管摩擦係数×管長÷管径)×(平均流速の2乗÷2×重力) | $⊿h=λ\frac{l}{d}$$×$$\frac{ν^2}{2g}$ |
| 動圧に比例する。 | ||
正解:⑵
