令和2年度A[問題 No.6]
[問題 No.6]流体に関する用語の組み合わせのうち、関係のないものはどれか。
(A) (B)
⑴ダルシー・ワイスバッハの式 圧力損失
⑵ベンチュリー管 流量測定
⑶トリチェリの定理 毛管現象
⑷ウォーターハンマー 水柱分離
令和2年度A[問題 No.6]解答
⑴関係ある。
| 流体の運動 | ||
| 名称 | 数式及び注意点 | |
| 摩擦応力 | 摩擦応力=粘性係数×速度勾配 | 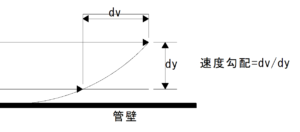 |
| 摩擦応力は速度勾配に比例する | ||
| 粘性係数は、気体では温度の上昇とともに大きくなり、液体では温度の上昇とともに小さくなる。 | ||
| 動粘性係数 | 動粘性係数=粘性係数÷密度 | $ν=\frac{η}{ρ}$ |
| 動粘性係数は、粘性係数に比例し、密度に反比例する。 | ||
| レイノルズ数 | レイノルズ数=平均流速×管径÷動粘性係数 | $Re=$$\frac{V×d}{ν}$ |
| 層流か乱流かを判断する数値 層流<2,000 乱流>4,000 | ||
| 慣性力(平均流速×管径)と粘性力(動粘性係数)の比で表す。 | ||
| レイノルズ数は、平均流速と管径に比例し、動粘性係数に反比例する。 | ||
| トリチェリの定理 | 流速=速度係数$\sqrt{2×重力加速度×水面の高さ}$ | $ν=C\sqrt{2gh} \\$ |
| 水槽の下端の小穴から流出する水の速度$ν$は、小穴から水面までの高さ$h$の1/2乗に比例する。 | 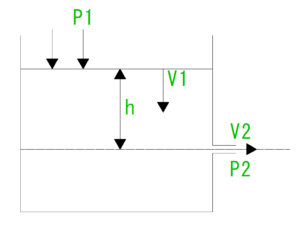 |
|
| 静圧 | 静圧=全圧-動圧 | $P$$S$$=$$P$$T$$-P$$D$ |
| 動圧 | 動圧=(流体の密度×流体の速度の2乗)÷2 | $P$$D$$=\frac{ρ×ν^2}{2}$ |
| 全圧 | 全圧=静圧+動圧 | $P$$T$$=P$$S$$+P$$D$ |
| 圧力損失 |
圧力損失=(管摩擦係数×管長÷管径)×(密度×平均流速の2乗÷2) | $⊿P=λ\frac{l}{d}$$×$$\frac{ρ×ν^2}{2}$ |
| ダルシー・ワイスバッハの式 | ||
| 管摩擦係数、管長、平均流速の2乗に比例する。 | ||
| 管径に反比例する。 | ||
| 水頭損失 |
水頭損失=(管摩擦係数×管長÷管径)×(平均流速の2乗÷2×重力) | $⊿h=λ\frac{l}{d}$$×$$\frac{ν^2}{2g}$ |
| 動圧に比例する。 | ||
⑵関係ある。
| 流量計 | |
| ピトー管 | 管内の全圧と静圧の差、動圧を測定して流量を算出する。 |
| ベンチュリー管 | 大口径部の静圧と小口径部の静圧の差を測定することにより流量を算出する。 |
| オリフィス流量計 | オリフィスの前後の静圧の差を測定することにより流量を算出する。 |
⑶関係ない。
トリチェリの定理図
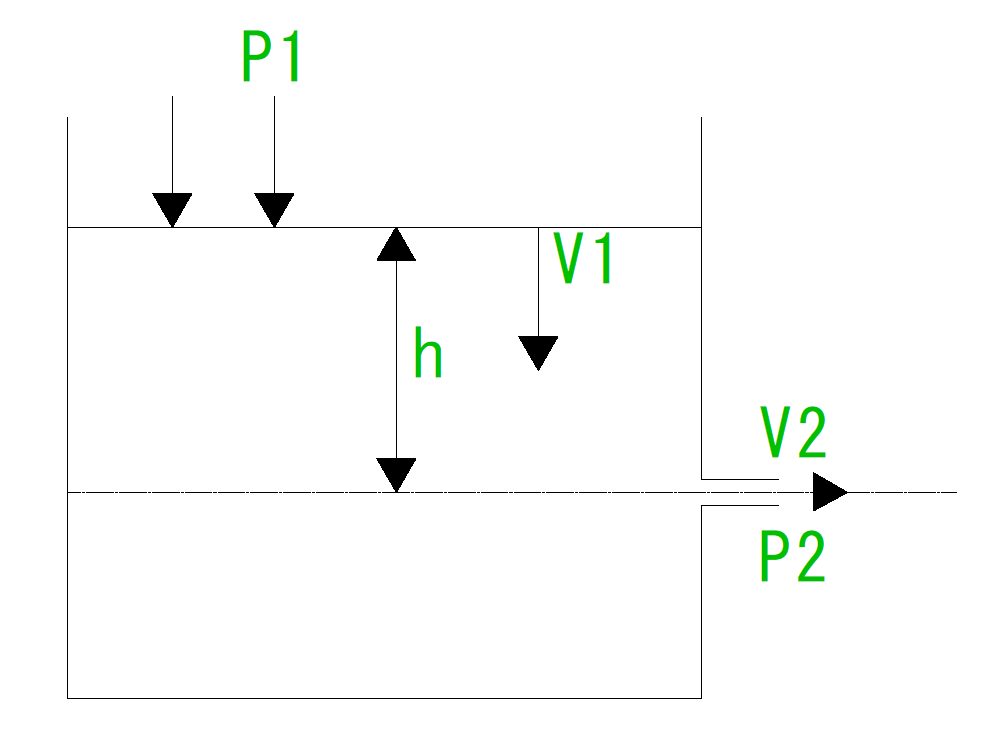
⑷関係ある。
揚水ポンプと高置水槽が平面的に離れている場合、揚水管までの横引きを最上階のような高い位置で行うと、揚水立て管の最上部付近で水柱分離が生じやすく、ウォーターハンマーが起こりやすい。水中分離は揚水ポンプが停止したときに、流れていた水の慣性力によって、管内に負圧が生じ、圧力がそのときの水の飽和水蒸気以下になると、その部分で水が蒸発し、水流が途切れて分離する現象である。
正解:⑶
